- Проекты
-
О телеканале
Деятельность
Обновления
- Телепрограмма
- Контакты
- Вещание
- Интернет-магазин
 Онлайн-трансляция
Онлайн-трансляция
Детский семейный образовательный телеканал
0+

 Помочь телеканалу
Задать вопрос
Оставить отзыв
Помочь телеканалу
Задать вопрос
Оставить отзыв
 Youtube «Школа Шишкиного Леса»
Youtube «Школа Шишкиного Леса»
 «Радость моя» детям
«Радость моя» детям
sof@))) ...
Усть-Каменогорск, 23 года
|
просмотров: 7247 | 0 |
Дорогая Соня, с удовольствием отвечу на твой вопрос, например: мама купила торт на обед. Торт разрезали на 8 долей. За обедом съели 3 доли. Осталось на блюде 5 долей торта. Эти пять долей обозначают: 5/8 торта.
Записи вида 5/8 называют обыкновенными дробями. В дроби число 5 называют числителем дроби, а число 8 — знаменателем дроби.
Знаменатель показывает, на сколько долей делят, а числитель — сколько таких долей взято.
Числитель дроби пишут над чертой, а знаменатель — под чертой.
Долю 1/2 называют половиной, 1/3 — третью, а 1/4— четвертью.??
Степан Петрович Круглов
Профессор математики
|
Саша ПетропЭ
|
просмотров: 3933 | 0 |
Дорогой Саша! Математически точного доказательства, что 2х2=5 нет, но есть решение, где хитрость и ошибка. Попробуй найти ошибку…
2*2=5
Доказательство:
то есть 4=5
25 - 45 = 16 - 36
Далее прибавим (9/2)^2 к обеим частям уравнения:
25 - 45 + (9/2)^2 = 16 - 36 + (9/2)^2
5^2 - (2*5*9)/2 + (9/2)^2 = 4^2 - (2*4*9)/2 + (9/2)^2
(5-9/2)^2 = (4-9/2)^2, обе части положительны, можно извлечь квадратный корень
5 - 9/2 = 4 - 9/2
Далее прибавим 9/2 к обеим частям уравнения:
5 = 4, что и требовалось доказать
Следовательно: 2*2 = 5??
Степан Петрович Круглов
Профессор математики
|
Дарья
|
просмотров: 7551 | 0 |
Дорогая Дарья! У овала нет сторон. Если тебя что-то интересует про овал, сформулируй, пожалуйста, свой вопрос иначе. Жду твоих писем.
посмотреть другие ответы
Альберт Петрович
|
Химик
|
просмотров: 2659 | 0 |
Здравствуй, дорогой друг!
В повседневной практике, даже при сложнейших вычислениях, редко используются числа больше миллиарда.
Миллиард — реже его называют биллионом — это единица с девятью нулями. Употребляется и триллион — единица с двенадцатью нулями. Наименования ещё больших чисел мало известны, да и ради экономии места они обозначаются и произносятся как степень числа 10. Например, десять в двадцать четвертой степени. Но у некоторых чисел-великанов названия есть:
10 5—квадриллион,
1018—квинтиллион,
1024—секстиллион,
1027—октиллион...
Американский математик Кастнер изобрел «самое большое число» и назвал его «гугол». Это единица со ста нулями! То есть, 10100.
Хотя естественный ряд чисел и бесконечен, всё же в известной мере гугол — это граница исчисляемого мира.
Жду твоих интересных вопросов.??
Альберт Петрович
|
Колосова Яна
село Твердилово.Оренбургская область.Бузулукский Район., 24 года
|
просмотров: 2618 | 0 |
Здравствуй дорогая Яна!
Для решения примеров с отрицательными числами, надо запомнить и понять несколько определений и правил.
Абсолютная величина (модуль). Для отрицательного числа – это положительное число, получаемое от перемены его знака с « – » на « + »; для положительного числа и нуля – само это число. Для обозначения абсолютной величины (модуля) числа используются две прямые черты, внутри которых записывается это число.
П р и м е р ы :
| – 5 | = 5,
| 7 | = 7,
| 0 | = 0.
Сложение:
1) при сложении двух чисел с одинаковыми знаками складываются их абсолютные величины и перед суммой ставится общий знак.
П р и м е р ы :
( + 6 ) + ( + 5 ) = 11
( – 6 ) + ( – 5 ) = – 11.
2) при сложении двух чисел с разными знаками их абсолютные величины вычитаются (из большей меньшая) и ставится знак числа с большей абсолютной величиной.
П р и м е р ы :
( – 6 ) + ( + 9 ) = 3
( – 6 ) + ( + 3 ) = – 3.
Жду твоих писем)))??
Альберт Петрович
|
Леушкин Юрий
ВКО, село Чапаево, 26 лет
|
просмотров: 4009 | 0 |
Здравствуй, Юрий. Задача о зёрнах на шахматной доске — математическая задача, в которой вычисляется, сколько будет зёрен на шахматной доске, если класть на каждую следующую клетку доски вдвое больше зёрен, чем на предыдущую, начиная с одного.
Для решения задачи учтём, что доска имеет 64 клетки. При удвоении количества зёрен на каждой последующей клетке сумма зёрен на всех 64 клетках составляет 18 446 744 073 709 551 615.
Хотя детали описания задачи в разных источниках отличаются, суть остаётся неизменной. Когда создатель шахмат показал своё изобретение правителю страны, тому так понравилась игра, что он позволил изобретателю право самому выбрать награду. Мудрец попросил у короля за первую клетку шахматной доски заплатить ему одно зерно пшеницы (по другой версии — риса), за второе — два, за третье — четыре и так далее, удваивая количество зёрен на каждой следующей клетке. Правитель, не разбиравшийся в математике, быстро согласился, даже несколько обидевшись за столь невысокую оценку изобретения, и приказал казначею подсчитать и выдать изобретателю нужное количество зерна. Однако, когда неделю спустя казначей всё ещё не смог подсчитать, сколько нужно зёрен, правитель спросил, в чём причина такой задержки. Казначей показал ему расчёты и сказал, что расплатиться невозможно. Правитель, чтобы взять реванш над пытавшимся его обхитрить изобретателем, велел последнему пересчитать каждое зёрнышко, чтобы не было сомнений в том, что он честно с ним расплатился.
Количество зерна примерно в 1800 раз превышает мировой объём урожая пшеницы за год.??
Альберт Петрович
|
ledi
|
просмотров: 4044 | 0 |
Дорогая Диана, Пифагор, VI в. до н. э. (580—500), — древнегреческий философ и математик, первым заложил основы математики как науки (в современном понимании этого слова)?, имел свою школу (школа Пифагора). Ему приписывают открытие так называемого правила Пифагора, хотя геометрическая интерпретация этой проблемы была известна и раньше в Египте и Вавилоне.
Развитие математики опирается на письменность и умение записывать числа. Наверно, древние люди сначала выражали количество путём рисования чёрточек на земле или выцарапывали их на древесине.
Древние инки, не имея иной системы письменности, представляли и сохраняли числовые данные, используя сложную систему верёвочных узлов, так называемые кипу.
Существовало множество различных систем исчисления.
Первые известные записи чисел были найдены в папирусе Ахмеса, созданном египтянами Среднего царства.
Индская цивилизация разработала современную десятичную систему исчисления, включающую концепцию нуля.??
Альберт Петрович
|
stas
зея
|
просмотров: 4003 | 0 |
Дорогой Станислав! Термин образован от лат. discriminar — «разбирать», «различать». Понятие «дискриминант квадратичной формы» использовалось в работах Гаусса, Дедекинда, Кронекера, Вебера и др.
Квадратным уравнением называется уравнение вида
ax2+bx+c=0 ,
где
x - переменная,
a, b, c - постоянные (числовые) коэффициенты.
В общем случае решение квадратных уравнений сводится к нахождению дискриминанта;
Формула дискриминанта:
D=b2-4ac
О корнях квадратного уравнения можно судить по знаку дискриминанта (D) :
D>0 - уравнение имеет 2 различных вещественных корня
D=0 - уравнение имеет 2 совпадающих вещественных корня
D
В общем случае корни уравнения равны:
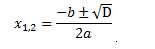
В случае с нулевым дискриминантом, оба корни равны
X1,2= - b/2a
Если коэффициент при х четный, то вычисляют не дискриминант, а четверть дискриминанта
D/4=(b/2)2- ac???
Альберт Петрович
|
Фуглаев Виталий
Старый Оскол Белгородская облась, 24 года
|
просмотров: 3058 | 0 |
Дорогой Виталий.
Окружность - замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая. Круг можно определить как часть плоскости, ограниченную окружностью.
Формула площади круга:
Площадь геометрической фигуры - часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади круга выражается числом заключающихся в него квадратных единиц.
1) Площадь круга равна произведению квадрата радиуса на число пи (3.1415)
S= πr2
2) Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.
S=Pr/2=1/2Pr
S - площадь круга
π - число пи (3.1415)
P – длина окружности
r - радиус круга
Формула периметра круга (длины окружности):
Периметр геометрической фигуры - суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.
1) Периметр круга равен произведению радиуса на два пи (3.1415)
P=2 πr
P - Периметр круга (длина окружности)
π - число пи (3.1415
r - радиус круга (окружности)
Радиус — не только величина расстояния, но и отрезок, соединяющий центр окружности с одной из её точек.
Отрезок, соединяющий две точки окружности, называется её хордой. Хорда, проходящая через центр окружности, называется диаметром.
посмотреть другие ответы
Альберт Петрович
|
Студенов Андрей
|
просмотров: 4339 | 0 |
Здравствуй, Андрей!
Начертим луч ОХ так, чтобы он шел слева направо

Отметим на этом луче какую-нибудь точку Е.
Над началом луча О напишем число 0, а над точкой Е — число 1. Отрезок ОЕ называют единичным отрезком.
Отложим далее на том же луче отрезок ЕА, равный единичному отрезку, и над точкой А напишем число 2. Затем на этом же луче отложим отрезок АВ} равный единичному отрезку, и над точкой В напишем число 3.
Так шаг за шагом получаем бесконечную шкалу. Ее называют координатным лучом.
Числа 0, 1,2, 3, ... , соответствующие точкам О, Е, A В, ... , называют координатами этих точек.
Пишут: О(0), Е(1), А(2), В(3) и т. д.
Альберт Петрович
|