- Проекты
-
О телеканале
Деятельность
Обновления
- Телепрограмма
- Контакты
- Вещание
 Онлайн-трансляция
Онлайн-трансляция
Детский семейный образовательный телеканал
0+

 Помочь телеканалу
Задать вопрос
Оставить отзыв
Помочь телеканалу
Задать вопрос
Оставить отзыв
 Youtube «Школа Шишкиного Леса»
Youtube «Школа Шишкиного Леса»
 «Радость моя» детям
«Радость моя» детям
Здравствуй, Диана. Магические кубы - это кубы с суммами чисел в рядах, параллельных граням и сумма чисел на диагоналях равны, (1+n3)n/2. Этот куб почти магический, так как суммы чисел любого из 3n слоёв и любого из 6 диагональных сечений равны, (1+n3)n/2.
Уникальность задания состоит в том, что нужно вписывать числа не в плоское, а в объёмное тело, поэтому нужно заполнять почти магический куб порядка, изучая каждый из n его слоёв.
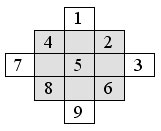
Начнём с известного алгоритма заполнения магического квадрата нечётного порядка на примере квадратов порядка 3 и 5:
Числа, не попавшие в заштрихованный квадрат, сдвигаем на n=3 единицы: 1 – вниз, 3 – влево, 9 – вверх, 7 – вправо. Получаем:
Аналогично заполняется магический квадрат порядка 5:
Важное наблюдение. Магические квадраты нечётного порядка, построенные описанным выше алгоритмом, обладают следующим свойством: нет ни одной строки и ни одного столбца в магическом квадрате, в которых стоят два сравнимых по модулю n числа.
Нам удалось отыскать универсальный алгоритм заполнения почти магического куба нечётного порядка. Рассмотрим в качестве примера почти магический куб порядка 3. Все три слоя куба пока пусты.

Шаг А. Вписываем числа от 1 до 9: число 1 вписываем в слой А, в ту клетку, где стояло число 1 в магическом квадрате (рис. 2); число 2 вписываем в ту клетку, где стояло число 2 в магическом квадрате (рис. 2), но уже в слое B; число 3 вписываем в клетку, где стояло число 3 в магическом квадрате (рис. 2), но в слое С; число 4 снова записываем в слое А, и так далее. Получаем:
Заметим, что в слое А находятся числа, сравнимые с 1 по модулю n, в слое В – числа, сравнимые с 2, в слое С – числа, сравнимые с 0.

Шаг B. Аналогично вписываем числа от 10 до 18, но заполнение начинаем теперь со слоя B: число 10 вписываем в слой B, в ту клетку, где стояло число 1 в магическом квадрате (рис. 2); число 11 вписываем в ту клетку, где стояло число 2 в магическом квадрате (рис. 2), но уже в слое С; число 12 вписываем в клетку, где стояло число 3 в магическом квадрате (рис. 2), но в слое A; и так далее. Получаем:
Шаг C выполняем аналогично предыдущим, но вписываем числа от 19 до 27 начиная со слоя С. Окончательно получаем слои почти магического куба порядка 3:
Нетрудно убедиться, что это действительно почти магический куб, – сумма чисел каждого из 9 слоёв и каждого из 6 диагональных сечений равна 162.
Желаю тебе хорошо учиться!