Академия занимательных наук. Математика. Вопросы

Здравствуй, Артур! Можно найти квадратный корень числа, но, скорее, подбором. Квадраты таких чисел, как 11, 12, 15 и некоторых других запоминаются наизусть. Затем ты смотришь, на что из этого твоё число похоже. Оно больше или меньше. И подбираешь корень. Ещё способ. Раскладываешь твоё число на множители, затем извлекаешь квадратный корень из каждого множителя и перемножаешь полученные результаты, чтобы найти ответ.

Здравствуй, Марина! Квадратный корень – это функция. Он определяется для всех положительных чисел. Обозначается значком √ . Квадратным корнем из числа а называется такое неотрицательное число х, квадрат которого равен а. Проще всего это понять на примере. √25 = 5. √169 = 13. √121 = 11. √16 = 4. Как его найти? Воспользоваться калькулятором или некоторые значения запомнить. Подбором можно найти. Например, √400 = 20. √389? Понятно, что ответ будет меньше, чем 20, но больше, чем 16, так как 16² = 256. Подбором определяем √389 = 19,72.

Привет, Андрей! Это такое число, которое при умножении само на себя даёт искомое. Проще всего это понять на примере: корень квадратный из 9 = 3, из 25 = 5, из 36 = 6, из 100 = 10,  из 169 = 13, а вот  корень из 34969 = 187. Подкоренное выражение всегда больше нуля, а вот сами корни могут быть и отрицательные. Корень из 9 = - 3. Квадратный корень нужен при решении квадратных же уравнений в восьмом классе и в некоторых других формулах, как составная часть. А также в экономике.

Здравствуй, Олег. 

Точным квадратным корнем из данного числа называется такое число, квадрат которого в точности равняется данному числу.

Если возведём в квадрат числа натурального ряда: 1, 2, 3, 4, 5 . . . , то получим такую таблицу квадратов: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144.

Для успешной работы с корнями достаточно знать квадраты чисел от 1 до 20. Причём туда и обратно. То есть ты должен легко называть как, скажем, 11 в квадрате, так и корень квадратный из 121.

Квадратные корни из отрицательных чисел извлечь нельзя! В школьном курсе математики принято считать за квадратные корни только неотрицательные числа. То есть ноль и все положительные.

Есть числа, которые в этой таблице не находятся. Из таких чисел, конечно, нельзя извлечь целый корень. Поэтому, если требуется извлечь корень из какого-нибудь целого числа, например, из числа 4082, то мы должны найти наибольшее целое число, квадрат которого заключается в 4082 (такое число есть 63, так как 63 в квадрате = 3969, а 64 в квадрате = 4090). Если данное число меньше 100, то корень из него находится по таблице умножения. Так, корень квадратный из 60 будет 7, так как 7 в квадрате равно 49, что меньше 60, а 8 в квадрате составляет 64, что больше 60.

Из многих чисел квадратные корни точно не извлекаются. Найдём, например, корень квадратный из двух - это число, которое при возведении в квадрат даст нам двойку. Только число это совсем неровное... Вот оно: 1,4143135… - эта дробь не кончается никогда... Такие числа называются иррациональным. Кстати, именно поэтому выражения с корнями называют иррациональными. Корень квадратный из 2 приблизительно равен 1,4. Корень квадратный из 3 приблизительно равен 1,7.

Дорогой Владимир,точным квадратным корнем из данного числа называется такое число, квадрат которого в точности равняется данному числу.

Если возведём в квадрат числа натурального ряда: 1, 2, 3, 4, 5 . . . , то получим такую таблицу квадратов: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144.

Для успешной работы с корнями достаточно знать квадраты чисел от 1 до 20. Причём туда и обратно. Т.е. ты должен легко называть как, скажем, 11 в квадрате, так и корень квадратный из 121.

Квадратные корни из отрицательных чисел извлечь нельзя! В школьном курсе математики принято считать за квадратные корни только неотрицательные числа! Т.е. ноль и все положительные.

Есть числа, которые в этой таблице не находятся; из таких чисел, конечно, нельзя извлечь целый корень. Поэтому, если требуется извлечь корень из какого-нибудь целого числа, например, из числа 4082 , то мы должны найти наибольшее целое число, квадрат которого заключается в 4082 (такое число есть 63, так как 63 в квадрате = 39б9, а 64 в квадрате = 4090). Если данное число меньше 100, то корень из него находится по таблице умножения; так, корень квадратный из 60 будет 7, так как 7 в квадрате равно 49, что меньше 60, а 8 в квадрате составляет 64, что больше 60.

Из многих чисел квадратные корни точно не извлекаются. Найдём, например, корень квадратный из двух - это число, которое при возведении в квадрат даст нам двойку. Только число это совсем неровное... Вот оно: 1,4143135… - эта дробь не кончается никогда... Такие числа называются иррациональным. Кстати, именно поэтому выражения с корнями называют иррациональными. Корень квадратный из 2 приблизительно равен 1,4. Корень квадратный из 3 приблизительно равен 1,7.

Здравствуй, Оля. Что такое квадратный корень?

Это понятие очень простое, естественное, я бы сказал. Математики на каждое действие стараются найти противодействие. Есть сложение - есть и вычитание. Есть умножение - есть и деление. Есть возведение в квадрат, значит, есть и корня! Вот и всё. Это действие (извлечение квадратного корня) в математике обозначается вот таким значком:

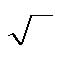
Сам значок называется красивым словом "радикал".

Как извлечь корень? Это лучше рассмотреть на примерах.

Как извлечь корень квадратный из 4? Нужно просто сообразить: какое число в квадрате даст нам 4? Да, конечно же, 2! Значит:

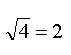
Сколько будет квадратный корень из 9? А какое число в квадрате даст нам 9? 3 в квадрате даст нам 9! Т.е:

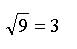
А сколько будет квадратный корень из нуля? Не вопрос! Какое число в квадрате ноль даёт? Да сам же ноль и даёт! Значит:

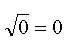
Возвести в квадрат можно любое число без особых проблем. Умножить число само на себя столбиком - да и все дела. А вот для извлечения корня такой простой и безотказной технологии нет. Приходится подбирать ответ и проверять его на попадание возведением в квадрат.

Для свободной и успешной работы с корнями достаточно знать квадраты чисел от 1 до 20. Причём туда и обратно.

Выражение, в котором под знаком квадратного корня стоит отрицательное число - не имеет смысла! Это запретная операция, такая же запретная, как и деление на ноль. Запомни этот факт! Или, другими словами: квадратные корни из отрицательных чисел извлечь нельзя?!