Академия занимательных наук. Математика. Вопросы

Здравствуй, Ангелина. Это происходит потому, что правильная дробь меньше 1. Пример: Если мы умножаем на ½, то это все равно, что разделить на 2, а если мы делим на ½, то это все равно, что умножить на 2. Желаю тебе хорошо учиться!

Здравствуй, Дима. Есть в математике специфические способы решения  квадратных уравнений и каких-либо дискриминантов.  Например,  один из таких приемов — теорема Виета. Для того, чтобы понять, как это делается, дадим следующее  определение.

Квадратное уравнение вида x² + bx + c = 0 будем называть приведенным. Коэффициент при x² равен 1. Никаких других ограничений на коэффициенты не даётся.

Вот основная теорема, для которой и даётся термин приведённого квадратного уравнения:

Теорема Виета. Мы имеем приведенное квадратное уравнение вида x² + bx + c = 0. Будем считать, что это уравнение имеет действительные корни x₁ и x₂. В этом случае верны следующие утверждения:

x₁ + x₂ = −b.  сумма корней приведенного квадратного уравнения будет равна коэффициенту при переменной x, взятому с противоположным знаком;

x₁ · x₂ = c. Произведение корней квадратного уравнения равно свободному коэффициенту.

Вот примеры:

x² − 9x + 20 = 0 ⇒x₁ + x₂ = − (−9) = 9; x₁ · x₂ = 20; корни: x₁ = 4; x₂ = 5;

x² + 2x − 15 = 0 ⇒x₁ + x₂ = −2; x₁ · x₂ = −15; корни: x₁ = 3; x₂ = −5;

x² + 5x + 4 = 0 ⇒x₁ + x₂ = −5; x₁ · x₂ = 4; корни: x₁ = −1; x₂ = −4.

Желаю тебе хорошо учиться.

Модуль числа  x называют расстояние (в отдельных отрезках) от точки начала координат до точки  x. Данное определение показывает геометрический смысл модуля.

Модуль действительного числа — это абсолютная величина этого числа.

При взятии модуля нужно отбросить от числа его знак.

Модуль числа a обозначается знаком |a|. Модуль числа всегда неотрицателен: |a|≥ 0.
|7| = 7, |-2| = 2, |9.5| = 9.5

Определение модуля:

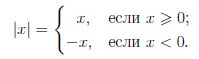
Модуль числа — это есть расстояние от нуля до данного числа.

Например, |-3| = 3. То есть расстояние от точки -3 до нуля равно 3.

Вот простейшее уравнение |x| = 3. На числовой прямой есть две точки (3 и -3), расстояние от которых до нуля равно трём. У уравнения |x| = 3 есть два решения: x = 3 и x = -3.

Пример 1.
|x — 3| = 4.

Это уравнение можно прочитать так: расстояние от точки x до точки 3 равна 4. По графикам можно понять, что уравнение имеет два решения: -1 и 7.

Пример 2.

Решим неравенство: |x + 7| < 4.

Оно читается как: расстояние от точки x до точки -7 меньше четырёх. Ответ: (-11; -3).

Пример 3.

Решаем неравенство: |10 — x| ≥ 7.

От точки 10 до точки   расстояние больше или равно семи. Ответ: (-∞; 3]υ [17, +∞)

Здравствуй, Георгий. Бесконечность - это абстрактное количественное обозначение чего-то большого, что не входит в  пространственные или временные границы. Бесконечность была предметом рассуждений философа Кантора. Ниже я привожу некоторые суждения из его ранней, как сейчас говорят, «наивной» теории множеств.

Нужно поставить на листке миллиметровки две точки. Дистанция между которыми конечна. В ходе наших рассуждений обнаружится, что ограниченный ими отрезок прямой заключает в себе бесконечность. И не одну. Можно поставить между двумя точками третью. Так же поделите надвое каждую из половинок, затем четвертушек, осьмушек и т. д. Теснее и теснее будут ложиться точки. Однако так и не удастся сделать из многоточия сплошную линию. «Татуирование» листа может продолжать бесконечно. Потому что ни одна из точек не будет последней. Всегда можно сделать что-то ещё - разделить пополам оставшиеся отрезочки, как бы малы они ни были. Желаю тебе хорошо учиться!

Здравствуй, Диана. Магические кубы - это кубы с суммами чисел в рядах, параллельных граням и сумма чисел на диагоналях равны, (1+n3)n/2. Этот куб почти магический, так как суммы чисел любого из 3n слоёв и любого из 6 диагональных сечений равны, (1+n3)n/2.

Уникальность задания состоит в том, что нужно вписывать числа не в плоское, а  в объёмное тело, поэтому нужно заполнять почти магический куб порядка, изучая каждый из n его слоёв.
Начнём с известного алгоритма заполнения магического квадрата нечётного порядка на примере квадратов порядка 3 и 5: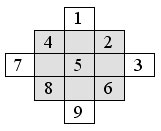

Числа, не попавшие в заштрихованный квадрат, сдвигаем на n=3 единицы: 1 – вниз, 3 – влево, 9 – вверх, 7 – вправо. Получаем:

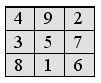
Аналогично заполняется магический квадрат порядка 5:

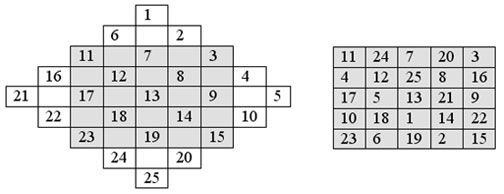
Важное наблюдение. Магические квадраты нечётного порядка, построенные описанным выше алгоритмом, обладают следующим свойством: нет ни одной строки и ни одного столбца в магическом квадрате, в которых стоят два сравнимых по модулю n числа.

Нам удалось отыскать универсальный алгоритм заполнения почти магического куба нечётного порядка. Рассмотрим в качестве примера почти магический куб порядка 3. Все три слоя куба пока пусты.

Шаг А. Вписываем числа от 1 до 9: число 1 вписываем в слой А, в ту клетку, где стояло число 1 в магическом квадрате (рис. 2); число 2 вписываем в ту клетку, где стояло число 2 в магическом квадрате (рис. 2), но уже в слое B; число 3 вписываем в клетку, где стояло число 3 в магическом квадрате (рис. 2), но в слое С; число 4 снова записываем в слое А, и так далее. Получаем:

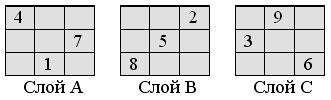
Заметим, что в слое А находятся числа, сравнимые с 1 по модулю n, в слое В – числа, сравнимые с 2, в слое С – числа, сравнимые с 0.
Шаг B. Аналогично вписываем числа от 10 до 18, но заполнение начинаем теперь со слоя B: число 10 вписываем в слой B, в ту клетку, где стояло число 1 в магическом квадрате (рис. 2); число 11 вписываем в ту клетку, где стояло число 2 в магическом квадрате (рис. 2), но уже в слое С; число 12 вписываем в клетку, где стояло число 3 в магическом квадрате (рис. 2), но в слое A; и так далее. Получаем:

Шаг C выполняем аналогично предыдущим, но вписываем числа от 19 до 27 начиная со слоя С. Окончательно получаем слои почти магического куба порядка 3:

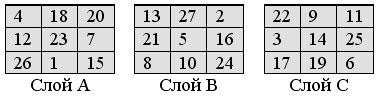
Нетрудно убедиться, что это действительно почти магический куб, – сумма чисел каждого из 9 слоёв и каждого из 6 диагональных сечений равна 162.

Желаю тебе хорошо учиться!

Здравствуй, Алина. Предлагаю такой способ: Надо взять маленький мячик и подбросить его вверх, при этом говорить : «2х2=4, 2х3=6, 2х4=8…» и так до тех пор, пока ты ошибаться перестанешь. Желаю тебе хорошо учиться.

Здравтствуй, Александр. Синус и косинус – это не числа, а тригонометрические функции.

Синус - отношение противолежащего катета к гипотенузе. Косинус - отношение прилежащего к гипотенузе. Значения посмотри в таблице Брадиса. Желаю тебе хорошо учиться.

Здравствуй, Серафима!

Модуль числа  x называют расстояние (в отдельных отрезках) от точки начала координат до точки  x. Данное определение показывает геометрический смысл модуля.

Модуль действительного числа — это абсолютная величина этого числа.

При взятии модуля нужно отбросить от числа его знак.

Модуль числа a обозначается знаком |a|. Модуль числа всегда неотрицателен: |a|≥ 0.
|7| = 7, |-2| = 2, |9.5| = 9.5

Определение модуля:

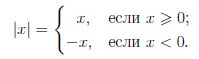
Модуль числа — это есть расстояние от нуля до данного числа.

Например, |-3| = 3. То есть расстояние от точки -3 до нуля равно 3.

Вот простейшее уравнение |x| = 3. На числовой прямой есть две точки (3 и -3), расстояние от которых до нуля равно трём. У уравнения |x| = 3 есть два решения: x = 3 и x = -3.

Пример 1.
|x — 3| = 4.

Это уравнение можно прочитать так: расстояние от точки x до точки 3 равна 4. По графикам можно понять, что уравнение имеет два решения: -1 и 7.

Пример 2.

Решим неравенство: |x + 7| < 4.

Оно читается как: расстояние от точки x до точки -7 меньше четырёх. Ответ: (-11; -3).

Пример 3.

Решаем неравенство: |10 — x| ≥ 7.

От точки 10 до точки   расстояние больше или равно семи. Ответ: (-∞; 3]υ [17, +∞)

Дорогая Милена! Цифр на свете всего десять, а самого последнего числа нет. Большие числа называются миллионы, миллиарды, биллионы и другие. Успехов тебе в учёбе.

Дорогой Друг! Пифагор был великим ученым, поэтому и теорема его верна.  В этой теореме говорится не про кратчайшее расстояние между двумя точками, а про площади. Площади двух квадратов, построенных на катетах треугольника, совпадают с площадью квадрата, построенного на гипотенузе. Одно из доказательств привожу ниже.

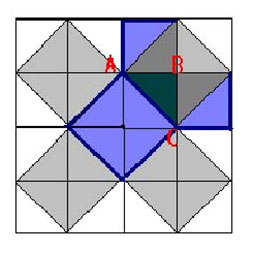
Простейшее доказательство теоремы:

Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников (рис.), чтобы убедиться в справедливости теоремы. Например, для треугольника  ABC: квадрат,построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах,— по два.

Теорема доказана.

Успехов тебе в учёбе.