Академия занимательных наук. Математика. Вопросы

Здравствуй, Максим.

Наиболее известные невозможные фигуры: невозможный треугольник, бесконечная лестница и невозможный трезубец.

«Отцом» невозможных фигур является шведский художник Оскар Реутерсвард, который за годы своего творчества нарисовал тысячи таких фигур. Настоящую известность невозможные фигуры обрели, когда их изобразил на своих литографиях известный голландский художник Мауриц Корнелис Эшер.

Невозможными фигурами называются фигуры, которые можно нарисовать, но не создать в реальности. Первой невозможной фигурой стал треугольник.

Невозможная фигура — один из видов оптических иллюзий, фигура, кажущаяся на первый взгляд проекцией обычного трёхмерного объекта, при внимательном рассмотрении которой становятся видны противоречивые соединения элементов фигуры.

  Кубик Рубика - Самая популярная головоломка тысячелетия!  Существуют специальные алгоритмы, зная которые, ты без труда соберёшь кубик за очень короткое время, алгоритмы сборки выложены в интернете, посмотри и попробуй собрать.

Здравствуй, Анастасия.

Модуль положительного числа равен самому числу. Модуль отрицательного числа равен числу, ему противоположному. Модуль нуля равен нулю.

Модуль, ничего не делая с положительными числами и нулем, отнимает у отрицательных чисел знак "минус".

Модуль обозначается вертикальными черточками, которые пишутся с двух сторон от числа.

Например /5/ = 5; /-3/ = 3; /-2,3/ = 2,3 ; /0/ = 0; /

Противоположные числа имеют равные модули.  |-4| = |4|. В твоем примере : |5| +|-5|=5+5 так как |5|=5 , |-5|=5.

Здравствуй, Семён. Спасибо за задачку. Ответ: один человек берёт яблоко вместе с корзиной, а остальные трое просто по яблоку.

Здравствуй, Алина.

Пусть у нас есть такая задачка.

«Проезд на автобусе стоит 14 рублей. В дни школьных каникул для учащихся ввели скидку 25%. Сколько стоит проезд на автобусе в дни школьных каникул?»

Сколько будет один процент от 14 рублей? Одна сотая часть. То есть 14/100 = 0,14 рубля. А таких процентов у нас 25. Вот и умножим 0,14 рубля на 25. Получим 3,5 рублей.  Величину скидки в рублях мы установили, остаётся узнать новую стоимость проезда:

14 – 3,5 = 10,5. Десять с половиной рублей. Это ответ.

Решим еще одну задачу - «Красивая тетрадка летом стоила 40 рублей. Перед началом учебного года, продавец поднял цену на 25%. Однако, тетрадки стали покупать так плохо, что он снизил цену на 10%. Всё равно не берут! Пришлось ему снизить цену ещё на 15%. Вот тут торговля пошла! Какова была окончательная цена тетрадки?»

 Решаем. На сколько рублей продавец поднял цену? 25% от 40 рублей - это 10 рублей. То есть, подорожавшая тетрадка стала стоить 50 рублей. Это понятно.

А теперь нам надо сбросить цену на 10% от 50 рублей. От 50, а не 40! 10% от 50 рублей – это 5 рублей. Следовательно, после первого удешевления тетрадь стала стоить 45 рублей.

Считаем второе удешевление. 15% от 45 рублей (от 45, а не 40, или 50!) – это 6,75 рубля. Стало быть, окончательная цена тетрадки:  45 – 6,75 = 38,25 рубля.

Здравствуй, Андрей. Твой вопрос очень интересный. 

Шарик, надутый обычным воздухом,  вообще не сможет полететь вверх. Взлететь в небо способен только воздушный шарик, надутый гелием. Такой шарик будет подниматься ввысь быстро и легко. Однако, по мере удаления от Земли снижается плотность воздуха, потому шарик через некоторое время остановится в определенной точке, где показатели плотности воздуха и плотности гелия сравняются.

Исследователи провели эксперименты и установили, что шарик с гелием остановится на расстоянии тридцати двух километров от Земли. Достигнув этой границы, он либо будет опускаться по мере того, как будет улетучиваться гелий, либо через какое-то время просто лопнет.

Здравствуй, Лаврентий. Это выражение - шуточное название одного из доказательств теоремы Пифагора.

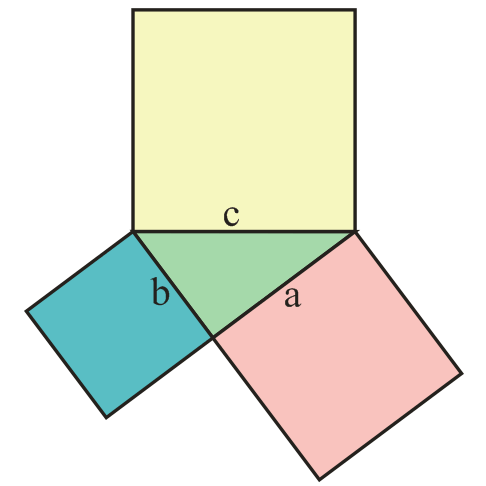Доказательство строилось на квадратах которые по виду напоминали штаны, отсюда и пошло это название, а теорема Пифагора утверждает что сумма квадратов катетов равна квадрату гипотенузы.

Здравствуй, Глеб. Наши современные цифры имеют арабское происхождение. В арабскую культуру они попали из Индии.  Арабские цифры не совсем воспроизводят индийские, поскольку арабы видоизменили их и приспособили  к своему письму.