Академия занимательных наук. Математика. Вопросы

Дорогая Евгения, постараюсь быть тебе полезным. Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны. Дано:

треугольник АВС,

треугольник А1В1С1,

АВ = А1В1,

АС = А1С1,

ВС = В1С1.

Доказать: треуг. АВС = треуг. А1В1С1.

Доказательство: Наложим треуг. АВС на треуг. А1В1С1 так, чтобы вершина А совместилась с вер- шиной А1, вершина В – с вершиной В1, а вершины С и С1 оказались по разные стороны от прямой А1В1 (рис. 1).

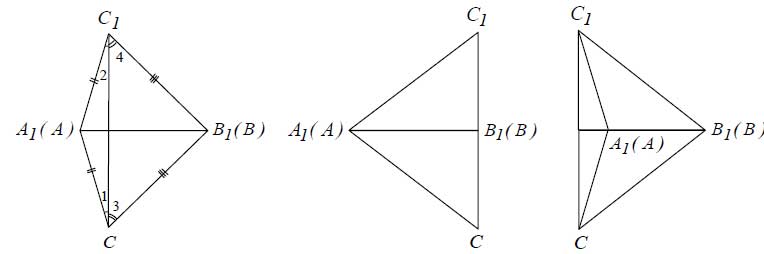
Возможны три случая: Рис.1

1) луч СС1 проходит внутри треуг. А1С1В1

2) луч СС1 совпадает с одной из сторон треуг. А1С1В1

3) луч СС1 проходит вне треуг. А1С1В1.

Рассмотрим случай, когда луч СС1 проходит внутри треуг. А1С1В1, остальные случаи доказываются аналогично.

По условию теоремы АС = А1С1, ВС = В1С1, поэтому треуг. А1С1С и треуг. В1С1С – равнобедренные по определению равнобедренных треугольников. По теореме о свой- стве углов при основании равнобедренного треугольника угол 1= углу 2, угол 3 = углу 4, поэтому угол 1 +угол 3 = угол 2 +угол 4, то есть угол C = углу C 1.

Получили, что АС = А1С1, ВС = В1С1 – по условию теоремы, угол С = углуС1- по доказанному, следовательно, треуг. АВС = треуг. А1В1С1 по I признаку равенства треугольников, по двум сторонам и углу между ними.

Итак, если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.

Всегда рад твоим письмам.

Дорогой Лёша, постараюсь тебе помочь:?

 1.  Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго плюс куб второго числа:

(a+b)³=a³+3a²b+3ab²+b³

2. Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго минус куб второго числа:

(a-b)³=a³-3a²b+3ab²-b³

Не надо путать эти формулы с формулами суммы кубов и разности кубов.

1. Сумма кубов двух числе равна произведению суммы этих чисел на их неполный квадрат разности.  Выражение (a²-ab+b²)   называют неполным квадратом разности. Перемножив сумму двух чисел на их неполный квадрат разности - получим формулу суммы кубов.

a³+b³= (a+b)(a²-ab+b²)

2. Разность кубов двух чисел равна произведению разности этих чисел на их неполный квадрат суммы. Выражение ( a²+ab+b²)  называют неполным квадратом суммы. Умножив разность двух чисел на их неполный квадрат суммы - получим формулу разности кубов.

a³-b³= (a-b)(a²+ab+b²).

Пиши, если что-то не понятно.

Здравствуй, Егор. Биссектриса (от лат. bi- «двойное», и sectio «разрезание») угла — луч с началом в вершине угла, делящий угол на две равные части.

Биссектриса угла (вместе с её продолжением) есть геометрическое место точек, равноудалённых от сторон угла (или их продолжений).

Биссектриса угла треугольника - это отрезок биссектрисы этого угла, соединяющий эту вершину с точкой на противолежащей стороне. Любая из трех биссектрис внутренних углов треугольника называется биссектрисой треугольника. Свойства биссектрис

1.Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон.

2.Биссектрисы внутренних углов треугольника пересекаются в одной точке. Это точка называется центром вписанной окружности.

3.Биссектрисы внутреннего и внешнего углов перпендикулярны.

Здравствуй, Сава.

Наиболее употребительные координатные системы - декартовы прямоугольные. Кроме прямоугольных систем координат существуют косоугольные системы, полярные системы координат - на плоскости, а в пространстве - цилиндрические или сферические системы координат. Например, координатные линии в полярных системах - окружности с центром в полюсе и лучи. Введение термина «полярные координаты» приписывают Грегорио Фонтана, жившему в XVIII веке в Италии.

Однако Грегуар де Сен-Венсан и Бонавентура Кавальери независимо друг от друга пришли к похожей концепции в середине XVII века. Сен-Венсан описал полярную систему в личных заметках в 1625 году. Это наиболее употребляемым системам координат в элементарной математике, есть формулы перехода из одной системы в другую. Но есть и реже используемые системы координат, например; биполярные координаты, бицентрические координаты, бицилиндрические координаты, конические координаты, параболические координаты, трилинейные координаты, эллипсоидальные координаты .

Здравствуй, Алдар.

Квадратура (лат. quadratura — придание квадратной формы) Слово квадратура имело разные значения на разных этапах развития математики и может означать следующее. 1.Построение квадрата, равновеликого данной фигуре (например, квадратура круга). Первоначальное античное понимание вычисления площади.

2. Число квадратных единиц в площади данной фигуры. Употребляется в основном в технике и быту («квадратура помещения 100 м²»).

3. Нахождение площади криволинейной фигуры.

Квадратура круга — задача, заключающаяся в нахождении построения с помощью циркуля и линейки квадрата, равновеликого по площади данному кругу. Наряду с трисекцией, является одной из самых известных неразрешимых задач на построение с помощью циркуля и линейки.

Здравствуй, Дима. Древнейшие древнеегипетские математические тексты относятся к началу II тысячелетия до н. э. Математика тогда использовалась в астрономии, мореплавании, землемерии, при строительстве домов, плотин, каналов и военных укреплений.

Развитие математики опирается на письменность и умение записывать числа. Наверно, древние люди сначала выражали количество путём рисования чёрточек на земле или выцарапывали их на древесине. Древние инки, не имея иной системы письменности, представляли и сохраняли числовые данные, используя сложную систему верёвочных узлов, так называемые кипу. Существовало множество различных систем счисления.

Первые известные записи чисел были найдены в папирусе Ахмеса, созданном египтянами. Индская цивилизация разработала современную десятичную систему счисления, включающую концепцию нуля.

Математика в современном понимании этого слова родилась в Греции. В странах-современниках Эллады математика использовалась для обыденных нужд (подсчёты, измерения). Жду твоих новых писем!

Здравствуй, Влада. Я отвечал на такой вопрос Владимиру Дерендяеву, посмотри ответ по ссылке.

Дорогая Yashma, самый перспективный материал А, так как он перспективнее В и С по условию твоей задачи.

Здравствуй, Мариночка! Для того чтобы перевести десятичную дробь в проценты надо умножить дробь на 100, например: 

0,35 *100=35% 0,18*100=18%.

Всегда рад твоим письмам.