Академия занимательных наук. Математика. Вопросы

Дорогая Настя, с удовольствием отвечу тебе на этот вопрос.

В Древнем Египте математики «настоящими» дробями считали только аликвотные дроби. Египтяне все дроби записывали как суммы долей, то есть дробей вида 1/n. Например: 8/15=1/3+1/5. Дроби 1/n  ( где n - натуральные число ), в современной математике именуются аликвотными ( от латинского aliguot- " несколько'').  То есть аликвотными дробями называются дроби с числителем 1. И даже сами аликвотные дроби египтяне часто стремились представить в виде суммы меньших аликвотных дробей. Например,     1/2=1/3+1/6, 1/4=1/5+1/20

Чтобы представить какое либо число в виде суммы аликвотных дробей, порой приходится проявлять, незаурядную изобретательность. Например, число 2/43 выражается так: 2/43= 1/42 +1/86 +1/129 +1/301. Существует формула, которая упрощает эту задачу.

1/n=(1/(n+1)) +(1/n*(n+1))

Примеры разложения дробей:

1/3=1/(3+1)+1/3*(3+1)=1/4 +1/12;      1/5=1/(5+1)+1/5*(5+1)=1/6 +1/30;

Но если преобразовать нашу формулу, то получим следующее полезное равенство:

1/(n*(n+1))=1/n -1/(n+1)

1/6=1/(2*3)=1/2 -1/3

½=1/(1*2)=1/1 -1/2

 Попробуем решить задачу:

1/2+1/(2*3)+1/(3*4)+1/(4*5)+…….+1/(19*20) =????

Воспользуемся нашей формулой для разложения аликвотной дроби в виде разности:

½=1/(1*2)=1/1 -1/2

1/6=1/(2*3)=1/2-1/3

1/12=1/(3*4)=1/3-1/4     и т.д.     1/20=1/(4*5)=1/4-1/5 

 Подставив, уже разложенные выражения в наш пример, получаем:

1/1-1/2+1/2-1/3+1/3-1/4+1/4-1/5……..+1/19-1/19-1/20=1/1-1/20=19/20.

Мы представили формулу, как удобство при разложении аликвотной дроби на 2 слагаемых. При разложении 1 на два слагаемых получается: 1=1/2+1/2 . Чтобы разложить 1 на 3 слагаемых, мы возьмем одну аликвотную дробь и по формуле разложим ее еще на две аликвотные дроби:  ½=1/3+1/6 => 1=1/2+1/3+1/6;

Чтобы разделить на 4 слагаемых, делим еще одну дробь на две аликвотные дроби:

1/3=1/4+1/12 => 1=1/2+1/4+1/12+1/6.

Здравствуй, Антон! С у довольствием помогу тебе с этой задачей.?

Трисекция угла — задача о делении заданного угла на три равные части построением циркулем и линейкой. Иначе говоря, необходимо построить трисектрисы угла — лучи, делящие угол на три равные части. 

Хотя трисекция угла в общем случае невыполнима с помощью циркуля и линейки, существуют кривые, с помощью которых это построение можно выполнить. Улитка Паскаля или трисектриса, Конические сечения, Спираль Архимеда.

Предположим, что имеется угол α = POM (рис. 1)

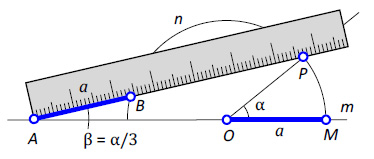
 Необходимо построить угол β, величина которого втрое меньше данного: α = 3β.

Продолжим сторону OM исходного угла и построим на ней как на диаметре окружность произвольного радиуса « a » с центром в точке O. Стороны угла пересекаются с окружностью в точках P и M. Возьмём линейку, отложив на ней величину « a » и используя прямую OM в качестве направляющей, точку P в качестве полюса, а полуокружность в качестве целевой линии, строим отрезок AB. Получим угол PAM, равный одной трети исходного угла α.

Доказательство; Рассмотрим треугольник ABO (рис. 2).

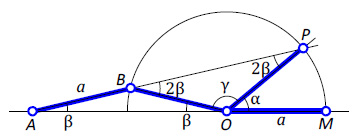
Так как AB = BO = a, то треугольник равнобедренный, и углы при его основании равны: ?BAO = ?BOA = β. Угол ?PBO как внешний угол треугольника ABO равен 2β.

Треугольник BPO также равнобедренный, углы при его основании равны 2β, а угол при вершине γ = 180°–4β. С другой стороны, γ = 180°–β–α. Следовательно, 180°–4β = 180°–β–α  ??

Здравствуй, Алена решим твою задачу. Пусть х см - сторона получившегося квадрата, тогда одна сторона прямоугольника была х+2 см, другая сторона была х+3 см. Площадь прямоугольника (х+2)(х+3) см², что на 51 см2 больше площади квадрата. Составляем и решаем уравнение:

(х+2)(х+3)-х²=51

х²+2х+3х+6-х²=51

5х=45

х=9 см - сторона получившегося квадрата.

Задача 1.  У Васи было на 10 марок меньше, чем у Коли. Каждый мальчик подарил Саше по 15 марок. У Васи осталось марок в 2 раза меньше, чем у Коли. По сколько марок было у мальчиков первоначально?  Попробуй решить самостоятельно. Жду твоих писем.

Задача 2.  Мать старше дочери в 2,5 раза, а 6 лет назад мать была в 4 раза старше дочери. Сколько лет матери и сколько лет дочери?

Здравствуй, Костя. Площадь всех фигур в геометрии вычисляется по определенным фрмулам. Для измерения параметров больших предметов используются различные измерительные приборы: рулетка, угломер, нивелир и т.д.

В настоящее время сущетвуют также и электронные приборы: лазерная рулетка, лазерный дальномер и т.д. С их помощью можно измерить длину, ширину и высоту разных предметов и вычислить их площадь по формулам. Жду твоих писем!

Здравствуй, Вадим. Давай решим твоё уравнение

7y+9-5y=13;

7у-5у+9=13;

2у+9=13;

перенесём число 9 на другую сторону уравнения, чтобы найти неизвестную величину y

2у=13-9;

2у=4,

следовательно у=2

Дорогой Артём, метод Гаусса очень интересный, но не очень простой. Гаусс Карл Фридрих (1777 - 1855). Выдающийся немецкий математик. Его труды  повлияли на развитие математической мысли, которая была неизменной многие столетия. Гаусс занимался основной теоремой алгебры о количестве корней алгебраического уравнения.

Метод Гаусса идеально подходит для решения систем содержащих больше трех линейных уравнений. Итак, метод Гаусса состоит из следующих шагов:

1.Рассмотрим первое уравнение. Выберем первый ненулевой коэффициент и разделим все уравнение на него. Получим уравнение, в которое некоторая переменная xi входит с коэффициентом 1;

2.Вычтем это уравнение из всех остальных, умножая его на такие числа, чтобы коэффициенты при переменной xi в остальных уравнениях обнулились. Получим систему, разрешенную относительно переменной xi, и равносильную исходной;

3.Если возникают уравнения (редко, но бывает; например, 0 = 0), вычеркиваем их из системы, в результате уравнений становится на одно меньше;

4.Повторяем предыдущие шаги не более n раз, где n — число уравнений в системе. Каждый раз выбираем для «обработки» новую переменную. Если возникают противоречивые уравнения (например, 0 = 8), система несовместна.

Через несколько шагов получим либо разрешенную систему, либо несовместную. Разрешенные системы распадаются на два случая:

1.Число переменных равно числу уравнений. Значит, система определена;

2.Число переменных больше числа уравнений. Собираем все свободные переменные справа — получаем формулы для разрешенных переменных. Эти формулы так и записываются в ответ.

Система линейных уравнений решена! Рассмотрим пример:

Решить систему уравнений:

х₁-х₂+х₃=6

х₁-2х₂+х₃=9

х₁-4х₂-2х₃=3

Решение:

1. Вычитаем первое уравнение из второго и третьего — получим разрешенную переменную x₂;

2.Умножаем второе уравнение на (−1), а третье уравнение делим на (−3) — получим два уравнения, в которых переменная x₃ входит с коэффициентом 1;

3.Прибавляем второе уравнение к первому, а из третьего — вычитаем. Получим разрешенную переменную x₃;

4.Наконец, вычитаем третье уравнение из первого — получаем разрешенную переменную x₁;

Получили разрешенную систему, записываем ответ. Ответ: x₁ = −1; x₂ = −3; x₃ = 4.

Здравствуй, Максим, точно неизвестно, кто придумал способ умножения чисел на 11, но в XIX в. французским математиком, специалистом по теории чисел Эдуардом Люка был опубликован четырёхтомный труд по занимательной математике, ставший классическим, там был описан этот способ умножения.

В 1891 году С.А. Рачинский издал книгу «1001 задача для умственного счёта», которая стала первым в России сборником упражнений по устному счёту, где был этот способ умножения двухзначного числа на 11.

Здравствуй, Ксения. Ты права 6.00=180 градусов, а вот 4.40=100 градусов –подумай и посчитай еще раз и внимательно посмотри программу. Она есть на сайте, выпуск номер 15. Жду твоих писем.

Здравствуйте, дорогие друзья. У многих чисел есть разные интересные свойства, например:

1 x 1 = 1

11 x 11 = 121

111 x 111 = 12321

1111 x 1111 = 1234321

11111 x 11111 = 123454321

111111 x 111111 = 12345654321

1111111 x 1111111 = 1234567654321

11111111 x 11111111 = 123456787654321

При умножении некоторых чисел на 7 получаются интересные произведения:

15873 • 7 = 111111

31746 • 7 = 222222

79365 • 7 = 555555

142857 •7 = 999999

Ещё один пример – при умножении чисел с семерками и девятками:

9 • 7 = 63

99 • 77 = 7623

999 • 777 = 776223

9999 • 7777 = 77762223

99999 • 77777 =7777622223

Жду ваших интересных писем!

Дорогой Владимир,точным квадратным корнем из данного числа называется такое число, квадрат которого в точности равняется данному числу.

Если возведём в квадрат числа натурального ряда: 1, 2, 3, 4, 5 . . . , то получим такую таблицу квадратов: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144.

Для успешной работы с корнями достаточно знать квадраты чисел от 1 до 20. Причём туда и обратно. Т.е. ты должен легко называть как, скажем, 11 в квадрате, так и корень квадратный из 121.

Квадратные корни из отрицательных чисел извлечь нельзя! В школьном курсе математики принято считать за квадратные корни только неотрицательные числа! Т.е. ноль и все положительные.

Есть числа, которые в этой таблице не находятся; из таких чисел, конечно, нельзя извлечь целый корень. Поэтому, если требуется извлечь корень из какого-нибудь целого числа, например, из числа 4082 , то мы должны найти наибольшее целое число, квадрат которого заключается в 4082 (такое число есть 63, так как 63 в квадрате = 39б9, а 64 в квадрате = 4090). Если данное число меньше 100, то корень из него находится по таблице умножения; так, корень квадратный из 60 будет 7, так как 7 в квадрате равно 49, что меньше 60, а 8 в квадрате составляет 64, что больше 60.

Из многих чисел квадратные корни точно не извлекаются. Найдём, например, корень квадратный из двух - это число, которое при возведении в квадрат даст нам двойку. Только число это совсем неровное... Вот оно: 1,4143135… - эта дробь не кончается никогда... Такие числа называются иррациональным. Кстати, именно поэтому выражения с корнями называют иррациональными. Корень квадратный из 2 приблизительно равен 1,4. Корень квадратный из 3 приблизительно равен 1,7.